Place Value Partitioning Numbers
Place Value
Are you teaching Place Value Partitioning? Do you need help and activities for Partitioning Numbers into tens and ones? Read on for resources, and valuable tips on teaching this mental math addition strategy, including why it’s important and common challenges students face.
What is Place Value Partitioning?
Partitioning numbers is all about breaking numbers into smaller, more manageable parts based on their place value; also known as Standard Partitioning.
In essence, it’s the process of decomposing a 2-digit number into its tens and ones components and a 3-digit number into hundreds, tens, and ones, and so on.
For example, in the number 46, the “4” represents 4 tens and the “6” represents 6 ones. And in the number 327, the “3” represents 3 hundreds and the “2” represents 2 tens and the “7” represent 7 ones. Non-standard partitioning is not used because it doesn’t use place value to split the numbers.
Teaching Place Value Partitioning
Place value partitioning is an invaluable mental math strategy that empowers students to tackle multi-digit calculations with ease. By teaching this strategy to your students they will learn to flexibly manipulate numbers and perform operations, especially addition and subtraction, more effectively.
Teaching students to break down numbers into their place value components allows them to mentally solve problems more efficiently. For example, when adding 36 and 48, students can decompose each number into tens and ones (30 + 6 and 40 + 8, respectively), add the tens and ones separately (70 + 14), and then combine the results to find the sum mentally.
This approach simplifies calculations, reduces cognitive load, and enhances numerical fluency. Through practice and mastery of place value partitioning, students develop a versatile mental math tool that empowers them to approach mathematical problems with confidence and efficiency.
Additionally, mastering partitioning lays the groundwork for understanding more complex concepts like regrouping and decimals.
Here’s a suggestion for a sequence of learning for teaching place value partitioning to students:
- Introduction: Start by introducing the concept of place value using concrete examples. For instance, show students the number 47 and explain that the “4” represents 40 and the “7” represents 7 ones. Use visuals like drawings or physical objects to represent this concept.
- Hands-on Manipulatives: Provide students with base ten blocks or bundles of pop sticks. Have them build numbers and decompose them into tens and ones. For example, students can represent the number 63 using 6 tens blocks and 3 ones blocks.
- Visual Representations: Use a place value chart to visually represent numbers and their place value. Have students fill in the chart to show the decomposition of numbers into tens and ones. For instance, on the chart, the number 58 would be represented as 5 tens and 8 ones.
- Guided Practice: Provide guided practice activities where students solve problems involving place value partitioning. For example, give students problems like “37 + 25” and guide them through the process of decomposing the numbers into tens and ones before adding them together.
- Independent Practice: Offer activities where students can practice place value partitioning independently. For instance, provide problems like 46 – 19 where students must decompose the numbers into tens and ones to solve the subtraction problem.
Student Difficulties
Students may encounter several challenges when learning to use place value partitioning, particularly in understanding the concept of breaking numbers into smaller parts based on their place value.
As Parish states,( 2010) “Teaching Place Value Partitioning is much more than requiring students to state how many hundreds, tens and ones are in a number or having them write a number in expanded notation, The true test of whether students understand place value is if they can apply their understanding in computation.”
Frequent issues students face include:
- Students lose track when counting large collections so check if errors are counting or place value-based
- Conceptual confusion, particularly in understanding the significance of place value and its application to everyday situations. For instance, when tasked with decomposing the number 63 into tens and ones, students might struggle to grasp why the “6” signifies 60 and the “3” represents 3 ones. While they recognise the association of “6” with 6 tens, linking it to a tangible quantity proves challenging for some students.
- Regrouping or exchanging values during partitioning. For example, when subtracting 29 from 53, students must regroup from the tens place to subtract accurately. However, some may incorrectly subtract 9 from 3 without regrouping, resulting in errors in their calculations. This difficulty in recognizing the need for regrouping can lead to inaccuracies in their mathematical work.
- Transitioning from concrete manipulatives to abstract number representations. For instance, when working with base ten blocks, students may easily understand that 37 can be represented as 3 tens blocks and 7 ones blocks. However, when asked to solve abstract mathematical problems involving place value, such as adding or subtracting multi-digit numbers, some students may struggle to apply this understanding effectively.
Overall, addressing these challenges requires patience, practice, and providing students with multiple opportunities to explore and manipulate numbers using place value partitioning strategies. By scaffolding their learning and offering support tailored to their individual needs, educators can help students overcome these obstacles and develop a deeper understanding of place value concepts.
Click to download the partitioning numbers activities below
Resources listed in this collection
Click to jump to...-
Mental Maths Activities Partitioning - Count Group & Circle Tens & Ones To 99 WORKSHEETS
-
Mental Maths Activities Partitioning - Group Tens & Ones To 99 WORKSHEETS
-
Mental Maths Activities Partitioning - Tens & Ones DECADES Task Cards
-
Mental Maths Activities Partitioning - Tens & Ones TEEN & TY Task Cards
-
Mental Maths Activities Partitioning - Tens & Ones To 100 Task Cards
-
Mental Maths Activities Partitioning - Tens & Ones To 100 Spinner Game WORKSHEETS
-
Mental Maths Activities Partitioning - Tens & Ones To 100 Spinner Games
2-Digit Partitioning
More Place Value Activities
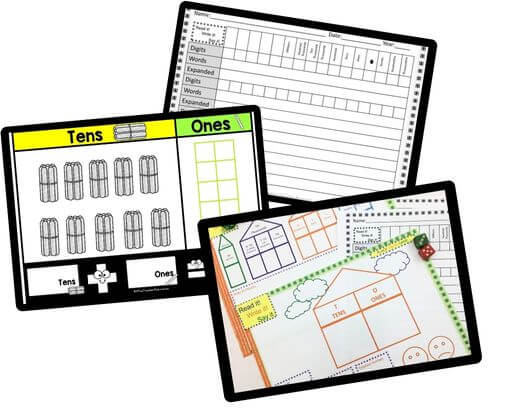
Place Value Boards

Place Value Games
Can't find what you're looking for?
Send us a request! Use this form to request a resource. Please give details of the learning area, topic, year level, curriculum links. We’ll be happy to take a look to see if we can fit it in. Unfortunately a request does not guarantee we will be able to make it!
"*" indicates required fields







